|
IN MEMORY OF NIKOLAI PAVLOVICH KORNEICHUK 
Nikolai Pavlovich Korneichuk passed away on July 22, 2003. He was recognized worldwide as a leading expert on exact solutions of extremal problems in Approximation Theory as well as a founder of a powerful research school. N.P.Korneichuk was born on January 22, 1920 in the village of Bobrik, in Gomel region of Belarus. His parents were peasants. In 1938, N.P.Korneichuk completed studies in the industrial and pedagogical technical school in Gomel. After that, he worked as a mathematics school teacher in the town of Turov. During the 1940s, N.P.Korneichuk served in the Soviet Army, fighting in the World War II. He was wounded twice and was decorated with the order of the Patriotic War of the 1st class and the order of the Red Star. After an honorable discharge from the army in 1949, N.P. Korneichuk worked as a mathematics school teacher in the town of Pavlograd in the Dnepropetrovsk region. Simultaneously, he studied extramurally at the Department of Physics and Mathematics of Dnepropetrovsk University. In 1955, he graduated magna cum laude from Dnepropetrovsk State University. It was exceptional case when an extramural student to obtained a magna cum laude degree. Following his graduation, N.P. Korneichuk successfully passed the entrance examinations to the graduate school of Dnepropetrovsk University and the same year he began graduate studies in mathematical analysis. His advisor M.D. Kalashnikov introduced him to the realm of ideas of the Approximation Theory school which was founded in Dnepropetrovsk by A.N. Kolmogorov and S.M. Nikolskii. One of the first research papers of N.P. Korneichuk received an award from Moscow State University. In 1959, N.P. Korneichuk defended his Candidate of Sciences (PhD) dissertation. Even though N.P.Korneichuk began his scientific career relatively late, it did not take him long to attract the attention of mathematical world. In 1961, he managed to solve the famous problem, posed by Favard, concerning the exact value of the best uniform approximation of Holder classes of periodic functions by trigonometric polynomials. Solving this problem alone made N.P.Korneichuk well-known both at home and abroad. The result of Dr.Korneichuk stood out among other exact results in approximation of functional classes with bounded highest derivative because it was not and could not be obtained via a linear method of approximation. N.P.Korneichuk pioneered an approach using intermediate approximation for the exact solution of the best approximation problem. First, he obtained sharp estimates on the deviation of classes NW∞1, N > 0, from Holder classes. To obtain estimates of the best approximation of the classes NW∞1 by trigonometric polynomials, he used Favards results. After that, summing both the estimations and minimising obtained the sum over N he obtained the solution of the Favard problem. Soon after, N.P.Korneichuk used his filigree technique to obtain the values of the error of best uniform approximation by trigonometric polynomials of the classes Hω. These classes are defined by a convex majorant ω of the modulus of continuity. Dr.Korneichuk showed that 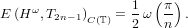 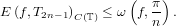 In 1963, N.P. Korneichuk successfully defended his Doctor of Physical and Mathematical Sciences dissertation at the meeting of the Scientific Council of the Mathematical Institute of the USSR Academy of Sciences. Note that it was only four years after the defense of his PhD dissertation. In the same year, he became the chair of the Department of Theory of Functions at Dnepropetrovsk State University. It was at this time when a scientific following of N.P. Korneichuk began to take shape up. His students of the Dnepropetrovsk period (till 1974) are A.I. Polovina, N.E. Lushpai, N.P. Horoshko, V.T. Martynyuk, V.P. Bugaets, V.P. Motornyi, V.L. Velikin, V.V. Lipovik, A.A. Zhensykbaev, L.G. Homutenko, I.I. Bezvershenko, V.F. Storchai, V.G. Doronin, V.I. Ruban, A.A. Ligun, V.F. Babenko. A characteristic trait of N.P. Korneichuk was his fascination and devotion to notoriously difficult problems whose solution required the creation of novel tools and approaches. As he said in the introduction to his first book ”Extremal Problems of Approximation Theory” (the one he liked himself the most): ”Attempts to solve some particular extremal problem usually somewhere very deep come to a problem which can be elementary formulated and which is connected to some simple-looking and intuitively very natural, but very hard to prove inequality. Here we need very delicate and deep analysis. We have to be able to find a new, non-standard, approach to investigate deep properties of functions of the class we consider.” Perhaps, the most notable scientific contribution of Prof.Korneichuk was his theory of Σ-rearrangements. Σ-rearrangements have common roots with Hardy’s decreasing rearrangements. In order to give a schematic definition of a Σ-rearrangement of a function, consider a representation of a given function as a sum of simple (i.e. unimodal and having compact support) functions. The sum of Hardy’s rearrangements of these simple functions is called a Σ-rearrangement of the given function. Hardy’s rearrangements are remarkable for the fact that they preserve the Lp-norm of a function for 1 ≤ p ≤∞. Σ-rearrangements of Korneichuk possess a different, equally remarkable, property of preserving both the L1-norm and the total variation of a function. Comparison theorems for Σ-rearrangements and Hardy’s rearrangements, proved by Prof. Korneichuk in 1970, as well as duality theorems formed the foundation for the new approach to extremal problems in Approximation Theory. This method allowed Prof.Korneichuk to solve the problem of approximating the classes WrHω with arbitrary r by trigonometric polynomials in uniform and integral norms. This approach also proved to be very fruitful in applications to many extremal problems in Approximation Theory and other areas of Analysis. In 1974, N.P. Korneichuk moved to Kiev where he became head of Department in the Institute of Mathematics of the National Academy of Sciences of Ukraine. There, he started educating and bringing up a new cohort of students. At the same time, N.P. Korneichuk did not lose his ties with Dnepropetrovsk, effectively being a head and coordinator of the research group in Approximation Theory at Dnepropetrovsk University. His students of the Kiev period (1974-2003) were N.A. Nazarenko, S.V. Pereverzev, M.Sh. Shabozov, A.M. Avakian, S.B. Vakarchuk, A.M. Minarchenko, Zh.E. Myrzanov, I.Ya. Tyrygin, A.L. Hizha, M.Yu. Savkina, O.V. Polyakov, S.G. Solodkyi, O.V. Motornaya, E.N. Gorohova. Note that most of them graduated from Dnepropetrovsk University. Mathematical methods and tools developed by N.P. Korneichuk had a profound impact on the development of Approximation Theory. Developing and perfecting these novel approaches, Prof. Korneichuk and his students tackled a series of long-standing extremal problems of Approximation Theory. Moreover, most results obtained within the past forty years in a number of areas of approximation theory significantly utilized Korneichuk’s ideas and results. These areas include approximation by polynomials and splines, optimization of quadrature formulae, n-widths of functional classes, optimal recovery of functions and functionals, one-sided approximation of functional classes, exact inequalities for the norms of intermediate derivatives (Landau – Kolmogorov type inequalities), extremal properties of polynomials and splines (splines of minimal defect, perfect splines, and monosplines). Since the nineties, Prof. Korneichuk’s primary interests were at the intersection of Approximation Theory with the theory of information. He realized that information driven approach to different approximation problems enabled more comprehensive usage of methods and results of Approximation Theory, especially in the problems of optimal reconstruction from incomplete data. Principal directions of N.P. Korneichuk’s work during this period were optimal recovery of functions and operators, especially adaptive recovery, complexity of approximation problems, and informational capacity of functionals. Besides that, he was interested in extremal problems of Approximation Theory and Analysis in general for multivariate functions. Along with being a successful researcher, Prof. Korneichuk was a prominent educator. His lectures were always admired by both students and faculty alike for their clarity and genuine fascination by the subject. These outstanding pedagogical abilities are also reflected in the several books authored by N.P.Korneichuk. The primary subject of these books was Approximation Theory, in particular, they summarized research of N.P.Korneichuk and his students. Immediately after publication, all these books achieved vast popularity among researchers specializing in Approximation Theory and Numerical Analysis. Such popularity is explained by both the high level of mathematical content and the exceptional clarity and accessibility of presentation, as well as meticulous selection of the material. One of his treatises was written by request of the world famous series ”Encyclopedia of Mathematics and its Applications” published by Cambridge University Press. All books in this series have to satisfy two criteria: the contents should be of imperishable interest and the clarity of the presentation should make the subject comprehensible to a general audience. The list of Prof. Korneichuk’s books includes:
Note that most of these books have been were translated into English, Spanish, Chinese. Nikolai Pavlovich Korneichuk was an outstanding person. Mathematical talent, crystal honesty, high responsibility and deep wisdom gained him respect and admiration everywhere. He liked literature, painting, sculpture, music, was interested in history. A wide range of research interests together with the unique combination of outstanding human qualities, pedagogical talent, and exceptional administrative abilities allowed Prof. Korneichuk to build an active and extremely productive research group. During the past 40 years, his research team was remarkably successful in different areas of Approximation Theory. At least half of the existing exact results in Approximation Theory belong to N.P. Korneichuk and his pupils. Over the years, students of Prof. Korneichuk produced about 30 candidate and 7 doctoral dissertations. Nowadays, members of his research team work successfully in Europe, Asia, and America. Scientific achievements of N.P. Korneichuk were valued highly both at home and abroad. In 1972, he was elected a corresponding member of the Academy of Sciences of Ukraine, and in 1998 – a full member. In 1973, Prof. Korneichuk was awarded the State Award of the USSR for the series of works on extremal problems of Approximation Theory. This was the first time when a Ukrainian mathematician received such an award alone. For his scientific achievements, N.P. Korneichuk was also decoreted by several orders and medals of the USSR. In 1994, he (along with S.M. Nikolskii and students) was awarded the State Award of Ukraine. This was for a series of works in spline theory and its applications in Approximation Theory. In 2001, Academician Korneichuk was awarded the Ostrogradsky prize. Exceptional personal qualities and mathematical talent of N.P. Korneichuk gained him high respect in the scientific community. For many years he served as the president of the Kiev mathematical society, vice academic secretary of the Department of Mathematics of the Ukrainian Academy of Sciences, head of the specialized committee on doctoral dissertations defense, editor-in-chief of many volumes on Approximation Theory edited in Dnepropetrovsk University and Institute of Mathematics of the Ukrainian Academy of Sciences, vice editor-in-chief of the Ukrainian Mathematical Journal, member of Editorial Board of ”East Journal on Approximations”, head of the expert committee of the Highest Attestations Committee. Until his last days N.P. Korneichuk carried on his work on classical problems of Approximation Theory and extremal problems of Analysis. Writing of two new books ”Approximations in the spaces with a cone” and ”Inequalities for derivatives of functions of small smoothness” was started due to his initiative and with his active participation. Everyone who knew Nikolai Pavlovich will cherish the memories of this remarkable person and scientist. V.F. Babenko, A.A. Ligun, V.P. Motornyi, N.A. Nazarenko, V.L. Velikin List of N.P. Korneichuk’s disciples with a Doctor of Science degree
|
